APGRADIENTTEST Procedure

@APGRADIENTTEST applies the Andrews and Ploberger(1994) change point analysis to a more general type of model than the linear regression than the @APBreakTest procedure allows. The input to this are the series of gradients from maximum likelihood estimation. These can be fetched using the DERIVES option on instructions like MAXIMIZE or GARCH.

@APGRADIENTTEST( options ) start end

# list of derivative series

Parameters

start, end

range for test. By default, the common range of the list of derivative series.

Options

PI=fraction of entries on ends of sample not examined as break points [.15]

This is written assuming PI is .15. A different "pi" value than .15 would require a different table of entries to compute the approximate p-values.

GRAPH/[NOGRAPH]

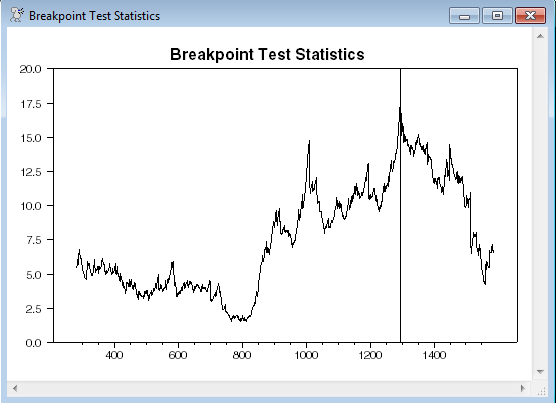
If GRAPH, the procedure produces a time-series graph of the breakpoint test statistics.

[PRINT]/NOPRINT

TITLE="title for output" ["Andrews-Ploberger Break Tests"]

Variables Defined

All are for the test on the full coefficient vector

%%BREAKPOINT	Entry with largest break test (INTEGER)
%%AQTEST	Andrews-Quandt test statistic (REAL)
%%APTEST	Andrews-Ploberger test statistic (REAL)
%%AQSIGNIF	Approximate significance value for AQ test (REAL)
%%APSIGNIF	Approximate significance value for AP test (INTEGER)

Example

This estimates a GARCH model, saving the derivatives and tests for breaks.

garch(p=1,q=1,hseries=hh11,derives=dd) / dlogdm

@apgradienttest(graph)

# dd

Sample Output

This starts with the output from the GARCH, since the order of the parameters in the test output is the same as on the GARCH.

GARCH Model - Estimation by BFGS

Convergence in 16 Iterations. Final criterion was 0.0000027 <= 0.0000100

Dependent Variable DLOGDM

Usable Observations 1866

Log Likelihood -2068.1265

Variable Coeff Std Error T-Stat Signif

************************************************************************************

1. Mean -0.020636536 0.015553819 -1.32678 0.18458061

2. C 0.016180183 0.005554235 2.91313 0.00357831

3. A 0.110126014 0.016373820 6.72574 0.00000000

4. B 0.868369483 0.020232859 42.91877 0.00000000

Andrews-Quandt Andrews-Ploberger

Test P-Val Date Test P-Val

1 12.982939 0.007 1296 3.623850 0.006

2 7.320293 0.090 1009 1.372721 0.117

3 3.224171 0.509 1296 0.518863 0.426

4 3.439964 0.468 1292 0.648551 0.341

All 18.171710 0.024 1296 5.499561 0.036

This indicates that there may be a problem with the mean of the model, which is the only parameter that shows a significant break.