BJIDENT Procedure

@BJIDENT assists in identifying a Box-Jenkins model by computing and graphing the correlations of the series in various differencing combinations.

@BJIDENT( options ) series start end

Parameters

series	series to analyze
start, end	range for calculations. By default, range of series

Options

DIFF=maximum regular differencings[0]

SDIFFS=maximum seasonal differencings[0]

TRANS=[NONE]/LOG/ROOT

Transformation to apply to data

SPAN=seasonal span

NUMBER=number of autocorrelations to compute [default depends upon data]

METHOD=YULE/[BURG]

Selects method used to compute correlations (see CORRELATE instruction for details)

REPORT/[NOREPORT]

QSTATS/[NOQSTATS]

REPORT shows a table with the ACF's and PACF's. When used with REPORT, QSTATS includes the Q-statistics in the report. The REPORT and QSTATS tend to be rather uninteresting at this phase of the analysis since it isn't expected that the series will be white noise or anything close to it.

[GRAPH]/NOGRAPH

Do graphs?

SPIKE/[NOSPIKE]

SPIKE selects a "spike" graph, rather than a bar graph, with the regular and partial autocorrelation graphs separated vertically.

SEPARATE/NOSEPARATE [default is NOSEPARATE except when using SPIKE]

Use SEPARATE if you want the correlations and partial correlations plotted as separate graphs (one a single page).

[ZERO]/NOZERO

Display the first correlation

MAX=maximum/minimum value on vertical axis scale [1]

Examples

This does @BJIDENT on a series with strong seasonality, so it includes both the DIFFS=1 and SDIFFS=1 options. This will produce autocorrelation graphs for (0,0), (0,1), (1,0) and (1,1) combinations of regular and seasonal differences.

open data aus_electric.xls

calendar(m) 1980

data(format=xls,org=columns) 1980:1 1995:8 elec

graph(header="Figure 7-9 Australian monthly electricity production")

# elec

* BJIDENT with both the DIFFS and SDIFFS option will do all combinations

* of 0 or 1 regular and 0 and 1 seasonal differences.

@bjident(diffs=1,sdiffs=1,method=burg,number=40) elec

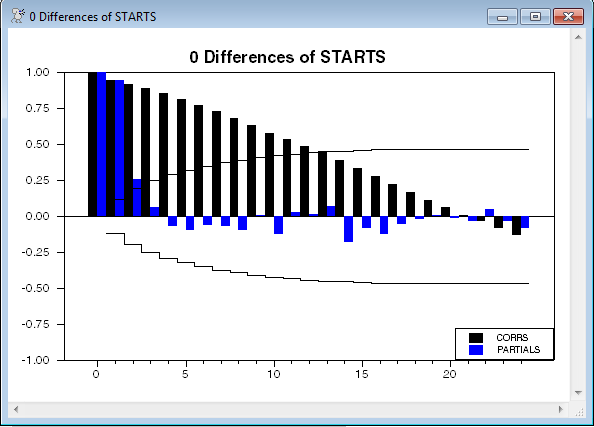
This does @BJIDENT on a series of housing starts. The output is shown below. For illustration, this includes the REPORT and QSTATS options, though there is little useful information in those. It's the graph of the correlations and partial autocorrelations that is most helpful. Here it would tend to show that the series is borderline between needing a difference, or being fit with an AR(2) as it stands.

open data house.dat

cal(m) 1968:1

data(format=prn,org=columns) 1968:1 1996:6

graph(key=upright,footer=$

"Figure 10.2. U.S. Housing Starts and Completions, 1968:01-1996:06") 2

# starts

# completions

@bjident(number=24,report,qstats) starts 1968:1 1991:12

Sample Output

As mentioned above, the report information generally isn't very useful, since there's no reason to suspect that the series (or any of its differences) will be serially uncorrelated, so the fact that the Q's are huge isn't a surprise.

0 Differences of STARTS

Lag Corr Partial LB Q Q Signif

1 0.940 0.940 256.988 0.000

2 0.913 0.254 500.281 0.000

3 0.886 0.065 730.153 0.000

4 0.850 -0.072 942.502 0.000

5 0.810 -0.096 1136.053 0.000

6 0.770 -0.061 1311.587 0.000

7 0.726 -0.071 1468.086 0.000

8 0.675 -0.099 1604.138 0.000

9 0.633 0.006 1723.939 0.000

10 0.575 -0.127 1823.413 0.000

11 0.531 0.031 1908.316 0.000

12 0.486 0.013 1979.661 0.000

13 0.447 0.072 2040.426 0.000

14 0.388 -0.178 2086.292 0.000

15 0.335 -0.085 2120.682 0.000

16 0.277 -0.123 2144.268 0.000

17 0.219 -0.055 2159.110 0.000

18 0.166 -0.020 2167.642 0.000

19 0.113 0.008 2171.630 0.000

20 0.062 -0.012 2172.842 0.000

21 0.008 -0.037 2172.864 0.000

22 -0.033 0.047 2173.208 0.000

23 -0.084 -0.036 2175.447 0.000

24 -0.132 -0.081 2181.000 0.000