|
Examples / UNION.RPF |
UNION.RPF is an example of estimation of probit, logit and linear probability models. This is adapted from Johnston and DiNardo(1997), pp 415-425. It analyzes the probability of union membership using a sample of 1000 individuals.
This first does a comparison of basic statistics for subsamples of union members and non-union members:
table(smpl=union,title="Statistics for Union Members") / $
potexp exp2 grade married high
table(smpl=.not.union,title="Statistics for Non-Union Members") / $
potexp exp2 grade married high
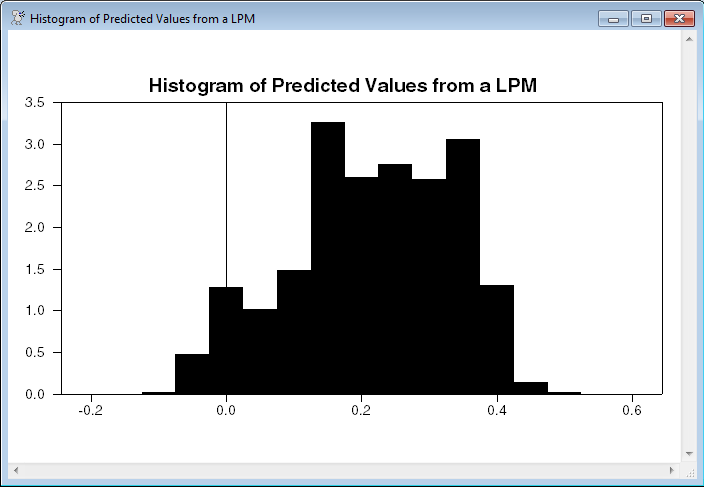
This fits a linear probability model and does a histogram of the predicted “probabilities”. (An LPM doesn't constrain the predictions to the \([0,1]\) range.) DENSITY with the option HISTOGRAM handles the counts for the histogram.
linreg union
# potexp exp2 grade married high constant
prj fitlp
density(type=histogram) fitlp / gx fx
scatter(style=bargraph,$
header="Histogram of Predicted Values from a LPM")
# gx fx
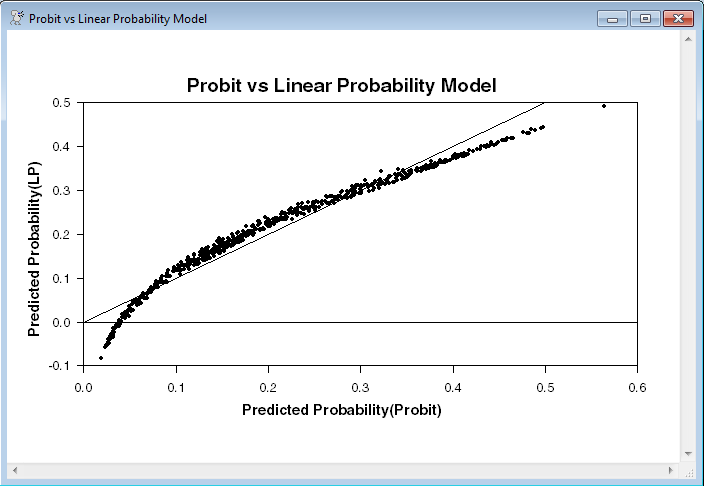
DDV estimates a probit model and shows a scatter graph of the predicted probabilities of the probit (computed using PRJ using the results of the probit estimation) vs. the LPM. The LINES=||0.0,1.0|| option on SCATTER puts a 45 degree line on the graph.
ddv(dist=probit) union
# potexp exp2 grade married high constant
prj(dist=probit,cdf=fitprb)
scatter(style=dots,lines=||0.0,1.0||,$
header="Probit vs Linear Probability Model",$
hlabel="Predicted Probability(Probit)",$
vlabel="Predicted Probability(LP)")
# fitprb fitlp
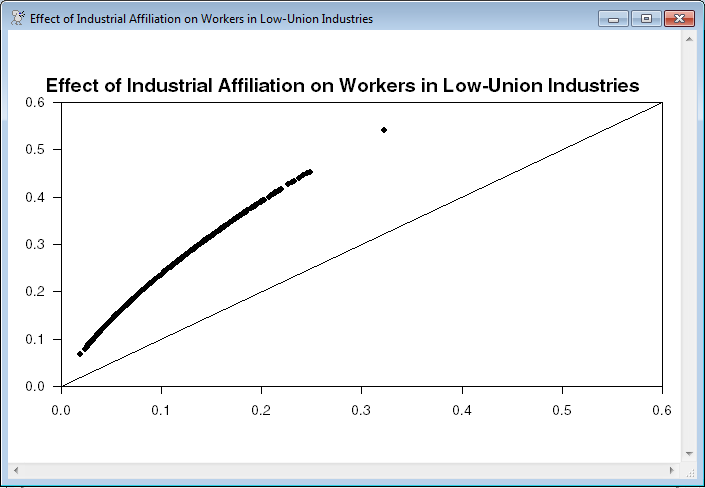
This evaluates the predicted effect of switching industries on individuals currently in low union industries. This is done by evaluating the predicted probabilities with the value of “high” turned on for all the individuals, then knocking out of the sample those who were already in a high union industry. The predicted probabilities are obtained by “dotting” the coefficients with the required set of variables, then evaluating the normal CDF (%CDF) at those values.
set z = %dot(%beta,||potexp,exp2,grade,married,1,1||)
set highprb = %if(high,%na,%cdf(z))
scatter(style=dots,vmin=0.0,lines=||0.0,1.0||,header=$
"Effect of Affiliation on Workers in Low-Union Industries")
# fitprb highprb
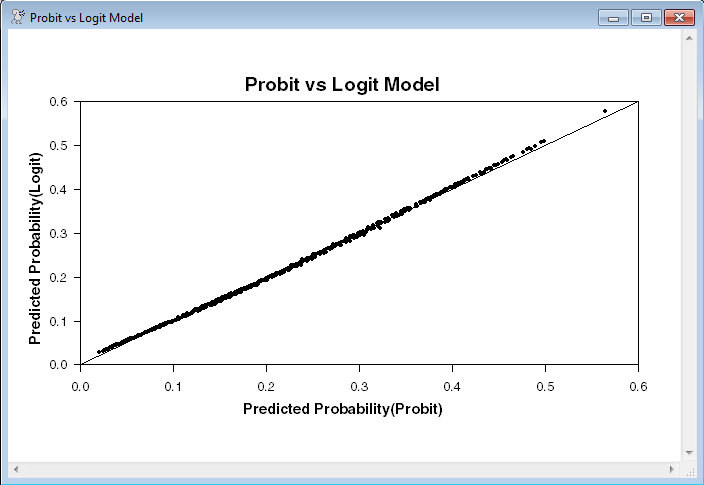
This re-estimates the model using logit rather than probit, and does a scatter graph comparing the probit and logit probabilities.
ddv(dist=logit) union
# potexp exp2 grade married high constant
prj(dist=logit,cdf=fitlgt)
scatter(style=dots,lines=||0.0,1.0||,$
header="Probit vs Logit Model",$
hlabel="Predicted Probability(Probit)",$
vlabel="Predicted Probability(Logit)")
# fitprb fitlgt
Full Program
open data cps88.asc
data(format=prn,org=columns) 1 1000 age exp2 grade ind1 married $
lnwage occ1 partt potexp union weight high
*
table(smpl=union,title="Statistics for Union Members") / $
potexp exp2 grade married high
table(smpl=.not.union,title="Statistics for Non-Union Members") / $
potexp exp2 grade married high
*
* Fit a linear probability model. Do a histogram of the predicted
* "probabilities".
*
linreg(title="Linear Probability Model") union
# potexp exp2 grade married high constant
prj fitlp
density(type=histogram) fitlp / gx fx
scatter(style=bargraph,header="Histogram of Predicted Values from a LPM")
# gx fx
*
* Probit model. Show a scatter graph of the predicted probabilites of
* the probit vs the LPM. Include the 45 degree line on the graph.
*
ddv(dist=probit) union
# potexp exp2 grade married high constant
prj(dist=probit,cdf=fitprb)
scatter(style=dots,lines=||0.0,1.0||,$
header="Probit vs Linear Probability Model",$
hlabel="Predicted Probability(Probit)",$
vlabel="Predicted Probability(LP)")
# fitprb fitlp
*
* Evaluate the predicted effect of switching industries on individuals
* currently in low union industries. This is done by evaluating the
* predicted probabilities with the value of "high" turned on for all the
* individuals, then knocking out of the sample those who were already in
* a high union industry. The predicted probabilities are obtained by
* "dotting" the coefficients with the required set of variables, then
* evaluating the normal cdf (%cdf) at those values.
*
set z = %dot(%beta,||potexp,exp2,grade,married,1,1||)
set highprb = %if(high,%na,%cdf(z))
scatter(style=dots,vmin=0.0,lines=||0.0,1.0||,$
header="Effect of Industrial Affiliation on Workers in Low-Union Industries")
# fitprb highprb
*
* Logit model
*
ddv(dist=logit) union
# potexp exp2 grade married high constant
prj(dist=logit,cdf=fitlgt)
scatter(style=dots,lines=||0.0,1.0||,$
header="Probit vs Logit Model",$
hlabel="Predicted Probability(Probit)",$
vlabel="Predicted Probability(Logit)")
# fitprb fitlgt
Output
Statistics for Union Members
Series Obs Mean Std Error Minimum Maximum
POTEXP 216 22.77777778 11.41710942 1.00000000 49.00000000
EXP2 216 648.57407407 563.34258574 1.00000000 2401.00000000
GRADE 216 12.56018519 2.27342339 5.00000000 18.00000000
MARRIED 216 0.75000000 0.43401854 0.00000000 1.00000000
HIGH 216 0.76388889 0.42567775 0.00000000 1.00000000
Statistics for Non-Union Members
Series Obs Mean Std Error Minimum Maximum
POTEXP 784 17.81122449 12.93830834 1.00000000 55.00000000
EXP2 784 484.42602041 595.76310328 1.00000000 3025.00000000
GRADE 784 13.13903061 2.67619124 0.00000000 18.00000000
MARRIED 784 0.61096939 0.48784152 0.00000000 1.00000000
HIGH 784 0.51403061 0.50012216 0.00000000 1.00000000
Linear Regression - Estimation by Linear Probability Model
Dependent Variable UNION
Usable Observations 1000
Degrees of Freedom 994
Centered R^2 0.0837275
R-Bar^2 0.0791185
Uncentered R^2 0.2816424
Mean of Dependent Variable 0.2160000000
Std Error of Dependent Variable 0.4117201884
Standard Error of Estimate 0.3950972711
Sum of Squared Residuals 155.16524249
Regression F(5,994) 18.1660
Significance Level of F 0.0000000
Log Likelihood -487.3062
Durbin-Watson Statistic 2.0015
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. POTEXP 0.020038767 0.003896914 5.14221 0.00000033
2. EXP2 -0.000370581 0.000081883 -4.52572 0.00000675
3. GRADE -0.012463581 0.005100452 -2.44362 0.01471364
4. MARRIED 0.013342779 0.030000989 0.44474 0.65660113
5. HIGH 0.143939577 0.025678520 5.60545 0.00000003
6. Constant 0.102136788 0.074933713 1.36303 0.17318220
Binary Probit - Estimation by Newton-Raphson
Convergence in 5 Iterations. Final criterion was 0.0000006 <= 0.0000100
Dependent Variable UNION
Usable Observations 1000
Degrees of Freedom 994
Log Likelihood -475.2514
Average Likelihood 0.6217287
Pseudo-R^2 0.0929077
Log Likelihood(Base) -521.7985
LR Test of Coefficients(5) 93.0941
Significance Level of LR 0.0000000
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. POTEXP 0.083509133 0.015608799 5.35013 0.00000009
2. EXP2 -0.001530796 0.000317877 -4.81569 0.00000147
3. GRADE -0.042077965 0.018908978 -2.22529 0.02606175
4. MARRIED 0.062251606 0.112583951 0.55293 0.58030792
5. HIGH 0.561295261 0.099662392 5.63197 0.00000002
6. Constant -1.468412409 0.295812594 -4.96400 0.00000069
Binary Logit - Estimation by Newton-Raphson
Convergence in 6 Iterations. Final criterion was 0.0000000 <= 0.0000100
Dependent Variable UNION
Usable Observations 1000
Degrees of Freedom 994
Log Likelihood -475.5541
Average Likelihood 0.6215406
Pseudo-R^2 0.0923048
Log Likelihood(Base) -521.7985
LR Test of Coefficients(5) 92.4887
Significance Level of LR 0.0000000
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. POTEXP 0.147402074 0.028097014 5.24618 0.00000016
2. EXP2 -0.002686919 0.000565428 -4.75201 0.00000201
3. GRADE -0.070320887 0.032142049 -2.18782 0.02868301
4. MARRIED 0.115463002 0.196778961 0.58676 0.55736156
5. HIGH 0.980141109 0.180049032 5.44375 0.00000005
6. Constant -2.581435857 0.518685883 -4.97688 0.00000065
Graphs
Copyright © 2025 Thomas A. Doan