Neural Networks

Artificial neural network (ANN) models provide a powerful alternative to standard regression techniques for producing time-series and cross-sectional models. Neural networks are particularly useful for handling complex, non-linear univariate and multivariate relationships that would be difficult to fit using other techniques.

Despite the fact that neural networks are simply a class of flexible non-linear functional forms, there has arisen a whole different set of terminology to describe their structure and the fitting process. While we present the standard neural network terms, we try also to provide a translation into a standard regression framework.

Overview of Neural Networks

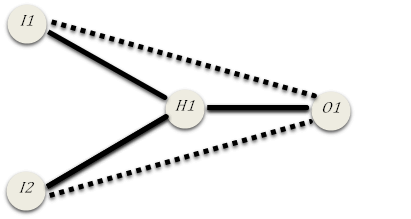
A neural network consists of an input layer containing one or more input nodes (in effect, the explanatory variables in a regression model), and an output layer of one or more output nodes (analogous to the dependent variable(s)). They normally also include a hidden layer, which lies between the input and output layers and consists of one or more hidden nodes.

Each input node is connected to each hidden node, and, in turn, each hidden node is connected to each output node. The model may also include direct connections between each input node and each output node. These can be used in addition to, or instead of, the hidden layer connections.

The diagram below represents a simple neural network with two input nodes (\(I_1\) and \(I_2\)), one hidden node (\(H_1\)), and one output node (\(O_1\)). The solid lines represent the connections between the input nodes and the hidden node, and between the hidden node and the output node. The dashed lines represent direct connections between the input nodes and the output node.

The hidden nodes and output nodes each have sets of weighting values associated with them. These serve the same purpose as the coefficients of a regression model. Given a set of input values, the weights determine the output(s) of the network.

In particular, each hidden node has a bias weight (intercept, in effect), plus separate input weights for each input node attached to it. In the example above, \(H_1\) would have three weights: a bias weight (which we’ll call \(h_{10}\)), the input weight associated with input \(I_1\) (\(h_{11}\)), and the input weight for \(I_2\) (\(h_{12}\)). Given the input values \(I_1\) and \(I_2\), the value of this hidden node would given by:

\begin{equation} u_1 = h_{10} + I_1 h_{11} + I_2 h_{12} \end{equation}

The actual output of the hidden node is determined by applying a “squashing” function to the value \(u\), which scales the output to range between zero and one.

Output nodes have a similar set of weights. For the example above, we would have \(o_{10}\) (the bias weight on output node 1), \(o_{11}\) (the weight of output node 1 for hidden node 1), \(d_{11}\) (weight of output node 1 on the connection with input node 1), and \(d_{12}\) (weight of output node 1 on the connection with input node 2). If we use a logistic squashing function for the hidden node, the output of this model would be:

\begin{equation} s_1 = {1 \mathord{\left/ {\vphantom {1 {\left( {1 + e^{ - u_1 } } \right)}}} \right.} {\left( {1 + e^{ - u_1 } } \right)}} \end{equation}

\begin{equation} O_1 = o_{01} + o_{11} s_1 + d_{11} I_1 + d_{12} I_2 \end{equation}

Fitting a neural network model involves “training” the model by supplying sets of known input and output values, and allowing the neural network algorithm to adjust the hidden node and output node weights until the output produced by the network matches the actual output in the training sample to the desired degree of accuracy.

Once trained, the model can then be used to generate new output data (fitted values or forecasts) from other sets of inputs. Assuming the fit is good, and that the relationships represented by the sample input and output data generalize to other samples, the model can produce good predictions.

However, care must be taken to avoid “overfitting” the model. This occurs when a network is trained to such close tolerances that it ends up modeling the “noise” in the training sample, not just the “signal.” Such a network will generally do a poor job of predicting appropriate output values for other sets of inputs. See below for details.

The NNLEARN and NNTEST instructions

The NNLEARN instruction is used to define a new neural network model, and to do additional training on an existing model. The NNTEST instruction is used to generate output (that is, fitted values) from a set of inputs, using a network model estimated using NNLEARN. For simple models, you may only need to use NNLEARN once to fit the network. For more complex models, you will often use NNLEARN and NNTEST in an iterative process, first training the model using NNLEARN, using NNTEST to generate output for comparison with training or validation samples, doing additional training as needed with NNLEARN, and so on.

SERIES variables are used for both the inputs and outputs on NNLEARN and NNTEST. This puts all of RATS’ data handling and transformation capabilities at your disposal in preparing data for neural network modeling, and for handling output. For example, you can: use the standard sample-range capabilities to train and test models using different samples; use standard lag or lead notation on the inputs for constructing time-series models; and graph fitted values against actual output.

The Backpropagation Algorithm

NNLEARN uses backpropagation techniques with an adaptive learning rate algorithm to train the model to a user-specified level of convergence. Translation: this is similar to steepest descent except that the derivatives for each weight are adjusted separately based upon the history of recent iterations. If you have more than one hidden node, the basic model isn’t identified in the standard statistical sense. Starting from randomized initial conditions, backpropagation does a lot of searching back and forth to find features for each of the nodes to pick up. This takes a lot of calculation, but allows the model to fit quite complex surfaces.

Because the entire process of fitting a neural network is so different from standard hill-climbing procedures, the options for controlling the process and determining convergence are different as well. For instance, there is an ITERATIONS option, but the required limit on this in most applications is quite large. The 100 or so that are usually the most required for a hill-climbing procedure will be far too small. NNLEARN does less calculation per “iteration” but also accomplishes less in terms of improving the fit (and may very well accomplish nothing). You might need tens or even hundreds of thousands of iterations to properly train a complex network.

Using NNLEARN

To create a neural net model, run the NNLEARN instruction with a set of input and output data, using the SAVE option to save the generated weights in a memory vector.

To do additional training on the same model, just do another NNLEARN instruction using the same memory vector on the SAVE option. You can either train on the same data set (perhaps setting a tighter convergence criterion or simply allowing more iterations if the desired criterion hasn’t been met), or you can train the model using other training samples (different entry ranges of the same input and output series, or entirely different input/output series). NNLEARN will use the existing values stored in the memory vector as starting values for the estimation. The new weights computed by NNLEARN will be saved back into the memory vector, replacing the previous values.

You may want to copy the contents of the memory vector to another array after each training step (with an instruction of the form COMPUTE array = memory vector). This allows you to go back to an earlier model if you find that subsequent training has resulted in overfitting. It also makes it easier to compare the outputs generated by the model at various stages of training.

You can also save memory vectors for use in a later session. Use OPEN COPY and WRITE(UNIT=COPY) to write the vector to a file, and DECLARE VECTOR, OPEN DATA and READ(VARYING) to read it back into memory.

Tips on Fitting Neural Network Models

As noted above, a potential pitfall of neural network models is that they are prone to “overfitting” the data. The goal in creating a neural network is to model accurately the underlying structural relationship between your input data and output data. If you use too many hidden nodes, or allow the model to train too long (if you use too tight a convergence criterion), your neural network may overfit the data, meaning that in addition to fitting the underlying signal, the network also models the noise in the training sample. Although an overfitted model will do an excellent job of modelling a particular training sample, it will often do a very poor job of modelling the general behavior of the process.

There are several ways to avoid overfitting. One is to make sure that you use only the minimum required number of hidden nodes. However, finding the optimal number of hidden nodes is often very difficult. If you end up using too few hidden nodes, the network will be unable to produce a good fit.

The other is to stop the training process before overfitting occurs. We would recommend that you use this method, because it is usually much easier to stop the training at the appropriate point than to try and determine the optimal number of hidden nodes. Also, this approach allows you to err on the side of having too many hidden nodes, rather than too few.

As suggested above, this is an iterative process, with the following basic steps:

1.Create and train the model using NNLEARN, with a fairly loose convergence criterion, and/or a relatively low limit on the number of iterations. Be sure to use the SAVE option to save the memory vector

2.Use a COMPUTE instruction to copy the current values of the memory vector to another array. Use a different name each time you do this step. If you find that you have overtrained the model, just go back to the memory vector saved previously and either use it as is, or do additional training (but to a looser criterion than the one that produced the overfitted model), or using a different set of training data.

3.Generate fitted values from the model using NNTEST with the estimated memory vector. Use graphs or PRINT instructions to compare the fitted and actual values. If you have a “validation” sample (a set of input and output values excluded from the training sample to be used to test the quality of the fit), use the validation sample inputs, and compare the resulting output to the validation sample outputs (by looking at the sum of squared errors, graph the validation and fitted values, etc.).

4.Repeat these steps until the desired fit is achieved. You can do additional training using the same set of sample inputs and outputs with a tighter convergence criterion (or higher iteration limit), or you can use additional training samples. Be sure to use the same memory vector on the SAVE option each time so the model starts up where it left off. However, by saving each set of weights into a different array in step (2), you’ll be able to go back to previous states if you find that the model eventually trains to the point of being overfit.

You are looking for the level of training that produces the minimum error when comparing network output to a separate validation sample. As the model fit improves with training, the errors should decrease steadily. At some point, however, the errors may begin to rise again, indicating that the model is probably starting to overfit the training sample (and thus providing a poorer fit for the validation sample).

We recommend that you always use the TRACE option to track the progress of the estimation. Some models will require tens of thousands or hundreds of thousands of epochs to produce a good fit. You may also find that NNLEARN sometimes reaches “plateaus” where the mean square error doesn’t change much for several thousand iterations, and then makes a significant improvement.

Also, be aware that the initial values used for the internal weights of a new network are determined randomly (if you aren’t using SAVE to supply an existing model and weights), so results will differ slightly from run to run. You can use the SEED instruction to seed the random number generator if you want the results of a program to be exactly reproducible.

Finally, you may occasionally run into situations where NNLEARN has trouble getting started, perhaps doing many thousands of epochs without making any significant progress. In such cases, you might want to interrupt and re-start the NNLEARN instruction in the hopes that a different set of initial values will perform better. However, these cases are fairly rare. In general, you simply need to be patient.

Convergence

To construct a useful neural network model, you will need to train the model sufficiently so that it models accurately the underlying behavior of the data, but not so tightly that it “overfits” the data used to train the model. That is, you want to model the “signal” present in your data, but not the noise.

RATS provides three options for controlling the convergence of the model. In most cases, you will use these options in an iterative process that involves invoking NNLEARN several times for the same model. The options available are:

iters=iteration limit [no limit]

cvcrit=convergence criterion [.00001]

rsquared=minimum R-squared level

The CVCRIT and RSQUARED options are mutually exclusive—they provide two ways of specifying the convergence criterion for the learning process. Both can produce equivalent fits, they simply offer different ways of thinking about the criterion. The default setting is CVCRIT=.00001 (if you use both, RATS will take the CVCRIT setting).

If you use the CVCRIT option, RATS will train the model until the mean square error (the mean of the squared error between the output series and the current output values of the network) is less than the CVCRIT value.

If you use the RSQUARED option, RATS will train the model until the mean square error is less than \(\left( {1 - R^2 } \right){\kern 1pt} {\kern 1pt} \sigma ^2 \), where \(R^2\) is the value specified in the RSQUARED option, and \(\sigma ^2 \) is the smallest of the output series variances.

The main disadvantage of CVCRIT is that it is dependent on the scale of the variables in the model. For example, suppose a CVCRIT of .0001 produces a good fit for a particular model. If you took the same model, but multiplied the output series by a factor of 10000, this CVCRIT setting would probably be much too tight.

The RSQUARED option is particularly handy for problems where you have a reasonable idea of what kind of “goodness of fit” you can expect from the model. Perhaps more importantly, the RSQUARED criteria is less dependent on the scale of the output because it is scaled by the output variance.

By default, NNLEARN will iterate until it satisfies the criteria set with CVCRIT or RSQUARED. You can use ITERS to place an upper limit on the number of iterations that NNLEARN will perform—it will stop iterating after the specified number of iterations, even if the criteria has not yet been met.

Padding the Output Range

The individual inputs are all rescaled internally to a range of [0,1]. In most cases, this will ensure that the coefficients are all within a few orders of magnitude of 1, which makes it easier to fit by backpropagation. Just as with any type of model that is fit to data, if you try to forecast values using explanatory variables that are far removed from those used in fitting (training) it, the results may be unreliable.

A more serious problem with neural nets, though, comes from the restriction on the range of the output variables. The rescaling of the inputs is done for convenience: since each has a freely estimated multiplicative coefficient wherever it appears, any scale choice can be “undone” by doing the opposite rescaling on the coefficients. However, the rescaling of the outputs is mandatory because of the use of the “squashing” function. If the output values are also rescaled to [0,1], then the network’s outputs will be constrained to the range from the training sample, since the squashing function can’t produce a value larger than 1. This will be a problem if you’re attempting to forecast a trending variable. To avoid this problem, you can use the option PAD=fraction to pad. This provides a value between 0 and 1 which indicates the fraction of “padding” to include when rescaling the output variables.

If, for instance, you choose PAD=.2, the smallest output value in the training sample will be mapped to .1 while the largest will be mapped to .9. If the original range of the data were from 7.2 to 8, this would allow the network to produce forecasts up to 8.1 and down to 7.1.

Examples

This example fits a neural network to the function:

\(y_t = \sin \left( {20x_t } \right)\) where \(x_t = .01,.02, \ldots ,1.00\)

You can experiment with this example to see the effects of changing the number of hidden nodes and/or the convergence criterion. We’ve used the CVCRIT option in this example—if you use RSQUARED, try a setting of about 0.8:

set input 1 100 = .01*t

set sinewave = sin(input*20)

nnlearn(hidden=6,save=memvec,trace,cvcrit=.01,ymax=1.0,ymin=-1.0)

# input

# sinewave

nntest / memvec

# input

# output

graph(key=below) 2

# sinewave

# output

This is an example from Tsay (2010, pp. 203–204). It fits a model with two hidden nodes and direct connection from inputs to the returns on IBM stock, using three lags as inputs. The sample through 1997:12 is used for training, while the sample from 1998 on is forecast.

nnlearn(rsquared=.10,iters=100000,hidden=2,direct,save=nnmodel) * 1997:12

# ibmln{1 2 3}

# ibmln

nntest 1998:1 1999:12 nnmodel

# ibmln{1 2 3}

# nnfore

@uforeerrors ibmln nnfore

NEURAL.RPF provides a complete example, fitting a neural net to a binary choice model. Like a probit model, the neural net attempts to explain the "yes" data given the characteristics of the individuals.