@RegCorrs performs an autocorrelation analysis on a series of residuals, similar to those typically done after estimating an ARIMA model.

@RegCorrs( options )   resids

Parameters

Options

NUMBER=number of autocorrelations to compute [depends upon number of data points]

METHOD=[YULE]/BURG
 

[GRAPH]/NOGRAPH

Graph the correlations

REPORT/[NOREPORT]

PRINT/[NOPRINT]

Include printed output from the correlations

 

TITLE="title of graph window and report window"

HEADER="header string for graph"

FOOTER="footer string for graph"

 

QSTATS/[NOQSTATS]

Computes and displays Ljung-Box Q Statistics

DFC=degrees of freedom correction for Q statistics

SPAN=width of test intervals [1]

 

[CRITERIA]/NOCRITERIA

Computes and displays the information criteria

 Variables defined

Example

This estimates an AR(7) model and uses @REGCORRS to examine the autocorrelation of the residuals. This uses the DFC=%NARMA option (%NARMA will be 7) to correct the degrees of freedom on the Q for the seven ARMA parameters used.

 

boxjenk(constant,ar=7) spread 1961:4 *

*

@regcorrs(dfc=%narma,number=20,qstats,report,$

   method=burg,title="AR(7) model diagnostics")

Sample Output

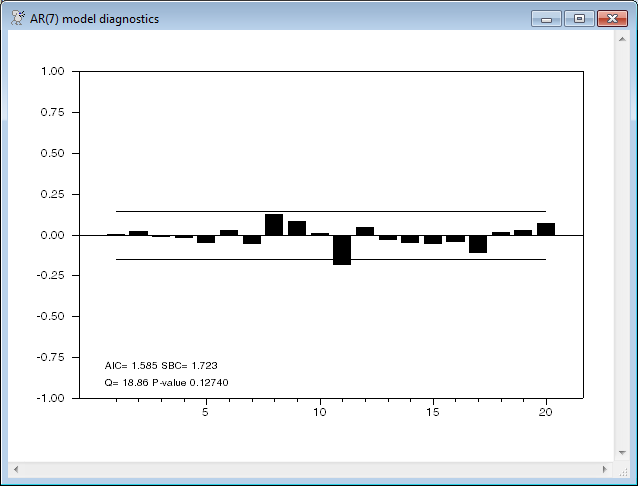
These are the results from the REPORT option. Note that the "Q Signif" is blank until lag 8 because 7 degrees of freedom are lost. After that, the Q's are floating around the standard rejection limit of .05. As you can see in the graph below, the AR(7) model manages to fairly well remove the autocorrelation of the first seven lags, but has problems just past that point.
 

Lag  Corr  Partial   LB Q    Q Signif

  1  0.000   0.000  0.000031

  2  0.024   0.024  0.108430

  3 -0.014  -0.014  0.146041

  4 -0.021  -0.022  0.230212

  5 -0.049  -0.048  0.688489

  6  0.026   0.027  0.820999

  7 -0.058  -0.056  1.470848

  8  0.124   0.122  4.501357    0.0339

  9  0.080   0.082  5.777170    0.0557

 10  0.012   0.003  5.803670    0.1216

 11 -0.184  -0.191 12.603911    0.0134

 12  0.048   0.051 13.071935    0.0227

 13 -0.033  -0.005 13.286264    0.0387

 14 -0.054  -0.063 13.877188    0.0534

 15 -0.061  -0.061 14.628409    0.0668

 16 -0.045  -0.063 15.045535    0.0897

 17 -0.111  -0.124 17.614942    0.0618

 18  0.016  -0.020 17.669738    0.0896

 19  0.030   0.088 17.862936    0.1199

 20  0.069   0.089 18.863287    0.1274

 

 

Copyright © 2026 Thomas A. Doan