Sweep Functions

The %SWEEP function, and related %SWEEPTOP and %SWEEPLIST functions, are very useful, and probably don’t get as much use as they deserve.

B=%SWEEP(A,k) is the following:

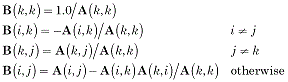
%SWEEP is reversible: %SWEEP(%SWEEP(A,k),k)=A.

The point of %SWEEP is the following: if A begins as a cross-product matrix of a set of variables, successive sweeps will do a regression. If we fix 1 as the dependent variable, after sweeping on 2 and 3, B(2,1) and B(3,1) will be the regression coefficients and B(1,1) will be the residual sum of squares. Note that the sweep operator does not produce a symmetric matrix.

The "sweep" functions are:

%sweep(A,k)	Returns the result of “sweeping” A on pivot k
%sweeplist(A,list)	Returns the result of “sweeping” A on each of the first k rows
%sweeptop(A,k)	Returns the result of “sweeping” A on each of the pivots listed in the VECT[INTEGER] IV

Consider the properties of the sweep function when applied to a cross product matrix:

1.The submatrix defined by the rows and columns of the pivots is \(({\bf{X}}'{\bf{X}})^{ - 1} \) from a regression on those variables.

2.The submatrix defined by the non-pivot columns with the pivot rows are the projection (regression) coefficients of the non-pivots on the pivots.

3.The submatrix defined by the pivot columns with the non-pivot rows are minus the projection coefficients.

4.The submatrix defined by the non-pivots by non-pivots gives the sums of the outer product of the projection residuals. (When divided by the number of observations, this will be the estimated covariance matrix of residuals).

If we take a regression of trend on constant,

set trend 1 10 = t

cmom

# constant trend

disp %sweep(%cmom,1)

The output is (with descriptions)

\(({\bf{X}}'{\bf{X}})^{ - 1} \) matrix	0.10000	5.50000	(regression coeff)
(–regression coeff)	-5.50000	82.50000	(Residual Sum of Squares)

One of the exercises in Hayashi(2000) is to do a Monte Carlo analysis of unit root tests, doing one Dickey-Fuller test allowing for intercept and one with intercept and trend. The sweep functions offer an efficient way to do this because the two regressions can be done by sweeping first on the lag and intercept, then again on the trend.

cmom

# y y{1} constant trend

We sweep on 2 and 3 to regress on Y{1} and CONSTANT. The regression coefficients are going to be in column 1 (non-pivot column). The sum of squared residuals is in (1,1). The t-stat can be put together using these and the (2,2) element.

compute ss=%sweeplist(%cmom,||2,3||)

compute tmu=(ss(2,1)-1)/sqrt(ss(1,1)*ss(2,2)/(%nobs-2))

Now sweep on the trend as well and repeat

compute ss=%sweep(ss,4)

compute ttau=(ss(2,1)-1)/sqrt(ss(1,1)*ss(2,2)/(%nobs-3))