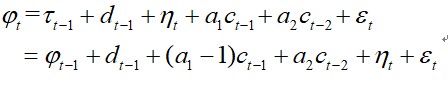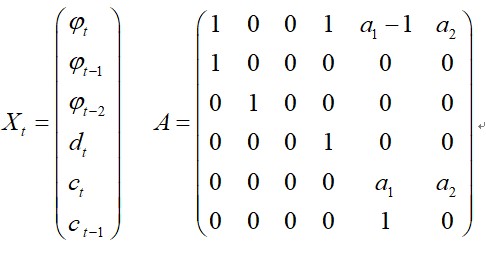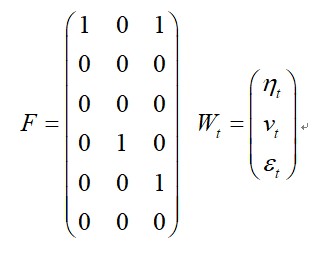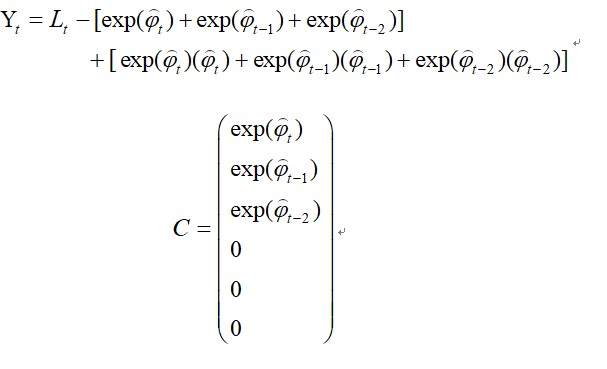Question on Log-linear Model

[hardmann]

Hi,
I was inspired by chapter 7 of Rats Handbook for State-Space Models, I try to use same method to handle my situation but not sure if it‘s right.

Assuming the distributed monthly GDP data are sum to the quarterly one:


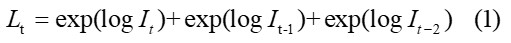
where log(I(t))=tau(t) +c(t), tau(t) is the unobserved trend, following RW(2) process：


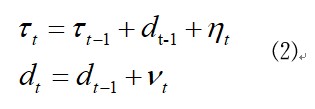
c(t) is unobserved cycle that follow AR(2) process：

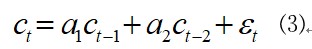
Where eta(t),nu(t),epsilon(t) all follow i.i.d normal distribution with zero mean.

I use multi dimensional taylor expansion to handle non-linear multi-variable equation (1)：

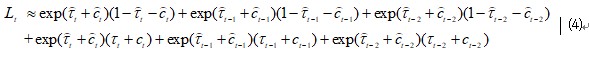
Then,I get a state space represtion of (1)-(4):

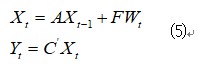
Where

W(t) follow normal distribution with zero mean.and covariance matrix R :



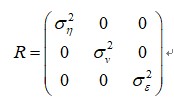
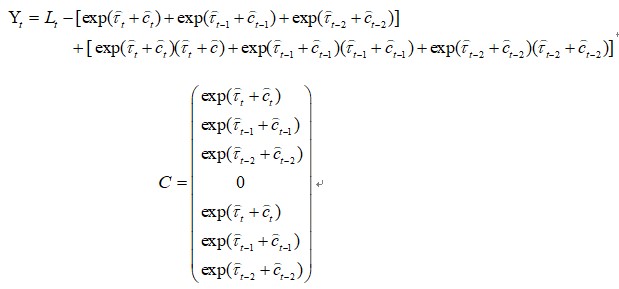
Problems:
(1)Does this method work?
(2)If it works ,for iteration 1,@Disaggregate seems to set log(y*lc(i)) as first xstate0 if I'm not misunderstand, what about my situation, how to set the initial value of tau(t) & c(t) ?

Thanks in advance for any help.

[TomDoan]

a. Your F matrix isn't quite correct. With d_t entering the tau equation, substituting out for it gives you both eta(t) and nu(t) components for tau.
b. You don't actually ever need the tau and c separately for the expansion, do you? They always occur as tau+c---for an initial guess of that you can just do a straight @DISAGGREGATE.

Offhand, I'm thinking that that is too broad a model. Even with a data set without two thirds of the "observations" being missing, the full I(2) trend + cycle models don't work well---probably it would make sense to eliminate the separate shock in the tau equation, since the cycle is really intended to model that part anyway.

[hardmann]

Dear Tom:

Thanks. I ignore a detail. If eq(2a) modified to tau(t)=tau(t-1)+d(t-1)+eta(t), is the F matrix correct?

Hardmann

[TomDoan]

Yes, with the dates corrected that way.

[hardmann]

Dear Tom:

For expansions, if we expand directly on log I(t0) instead of tau (t0) and C (t0) separately, I am not sure whether the results are different. If there is no difference, the expansion on log I(t0) is concise and effective.

Best regard
hardmann

[hardmann]

Hi Tom,
Thank you for your detailed reply.

Setting aside the problem of the model itself, I'm a little stuck on your advice,

b. You don't actually ever need the tau and c separately for the expansion, do you? They always occur as tau+c---for an initial guess of that you can just do a straight @DISAGGREGATE.

I found there are two interpretations about your suggestion. I am not sure if the following are what you really mean or whether there are some flaws.

a. Only treat tau and c as one during expansion(which lead to same result as separate one) and following the setting of X(t),A,F,W,Y(t),C above. Finally, do some initial value guessing that I don't figure out yet.

b. Set phi(t)=tau(t)+c(t)，Since

So I omit tau(t),set



Finally, set intial value as log(observed data* a weight that corresponding to MAINTAIN option).（Since there is only one variable in iteration process.)

With much appreciation,
H

[TomDoan]

You can rewrite the model, but the original point is that the non-linearity applies only to the sum of tau and c, so the derivatives in the linearization depend only upon the sum of tau and c, thus you don't actually need an initial guess for tau-tilde and c-tilde but just their sum. Once you've done one iteration, your model is generating tau-tilde and c-tilde (and thus their sum).

[hardmann]

Yes,of course! It’s so obvious, I can’t believe I didn’t figure it out until you reply patiently .Thanks again.

I tried to imitate @Disaggregate code to solve this model , since tau-tilde and c-tilde have different stationary properties,so there is a need to set g matrix in DLM.So how to set a g matrix that match corresponding state?

Thank you for your help.