Page 2 of 6
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Wed Jan 25, 2017 4:28 pm
by jack
I use this code (a part of the code):
Code: Select all
*
*
* Regime-switching GARCH
*
nonlin a01 a02 a11 a12 b01 b11 b21 b02 b12 b22 p
compute a01=%beta(1),a11=%beta(2),b01=olsvar,b11=0.0,b21=0.0
compute a02=%beta(1),a12=%beta(2),b02=%beta(3),b12=%beta(4),b22=%beta(5)
compute p=||.95,.05||
*
set uu = olsvar
set h = olsvar
*
* RegimeGARCHF returns the 2 vector of densities in the two regimes.
* Again, many lines in this are specific to the problem at hand.
*
function RegimeGARCHF t
type vector RegimeGARCHF
type integer t
local real hh1 hh2 mu1 mu2 mu
*
* Compute state dependent variances
*
compute hh1=b01+b11*uu(t-1)+b21*h(t-1)
compute hh2=b02+b12*uu(t-1)+b22*h(t-1)
*
* Compute state dependent means
*
compute mu1=a01+a11*rate(t-1)
compute mu2=a02+a12*rate(t-1)
*
* Compute the return vector (densities in the two states)
*
compute RegimeGARCHF=||%density((drate(t)-mu1)/sqrt(hh1))/sqrt(hh1),$
%density((drate(t)-mu2)/sqrt(hh2))/sqrt(hh2)||
*
* Compute the values of uu (squared residual) and h (variance) to be
* used for the period following.
*
compute mu=mu1*pstar(1)+mu2*pstar(2)
compute uu(t)=(drate(t)-mu)^2
compute h(t)=pstar(1)*(mu1^2+hh1)+pstar(2)*(mu2^2+hh2)-mu^2
end
*
frml logl = f=RegimeGARCHF(t),fpt=%MSProb(t,f),log(fpt)
*
* This combination is able to locate Gray's results - the first MAXIMIZE
* works with the "p" matrix fixed at a fairly high level of persistence,
* and tries to get estimates which separate the two states. The second
* then adds the p matrix to the parmset.
*
nonlin a01 a02 a11 a12 b01 b11 b21 b02 b12 b22
maximize(start=(pstar=%MSInit()),method=bfgs,iters=100,pmethod=simplex,piters=50) logl 2 *
nonlin a01 a02 a11 a12 b01 b11 b21 b02 b12 b22 p
maximize(start=(pstar=%MSInit()),method=bfgs,iters=100) logl 2 *
*
* Compute the smoothed probabilities and the ex ante probabilities
*
@MSSmoothed %regstart() %regend() psmooth
set exante %regstart() %regend() = pt_t1(t)(1)
set smooth %regstart() %regend() = psmooth(t)(1)
*
* And the conditional standard deviation
*
set condstddev = sqrt(exante*b01^2+(1-exante)*b02^2)
*
spgraph(vfields=2,window="Figure 5")
graph(max=1.0,header="Regime Probabilities") 2
# exante
# smooth
graph(header="Conditional Standard Deviation")
# condstddev
spgraph(done)
I did the calculations after the MAXIMIZE instruction for the MS-GARCH. But I'm not sure if I'm doing the right thing about H.
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Wed Jan 25, 2017 4:40 pm
by TomDoan
That's just repeating the values from the previous model. The MS-GARCH computes H as the ex-ante variance, and that's what you need:
set condstddev = sqrt(h)
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Wed Jan 25, 2017 4:58 pm
by jack
I really appreciate your kind replies and I'm so sorry for asking so many questions.
Here is the graph.
I would be grateful if I could possibly have your final word about it. Doesn't it mimic probabilities again?
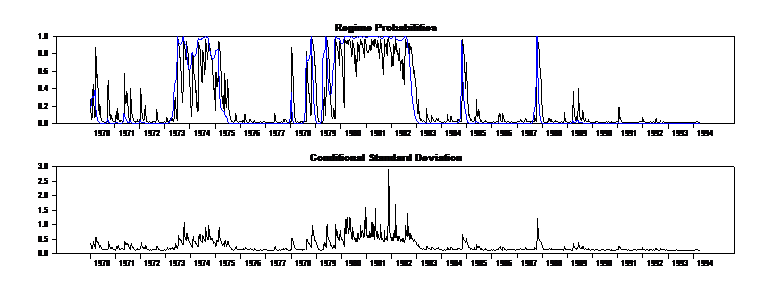
- figure 5.png (17.71 KiB) Viewed 47856 times
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Wed Jan 25, 2017 5:10 pm
by TomDoan
First of all, isn't that effectively the same graph as in the paper? But no, compare the 1980-1982 range. The probabilities are relatively flat and the standard deviations are very spiky. If you compare the graph with the switching by non-GARCH variances, where the probabilities are flat, so are the standard deviations.
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Thu Jan 26, 2017 2:25 pm
by jack
Dear Tom,
I searched for smoothed and ex ante probabilities and studied Gray's paper about it. Unfortunately, I didn't find a satisfactory answer for it. To be clear, I don't know what's the difference between them intuitively? Which one is more important?
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Thu Jan 26, 2017 2:43 pm
by TomDoan
I'm not sure there's any "intuition" involved. The ex ante probability at t uses only the observations before t. It's used in computing the likelihood and any diagnostics. The smoothed probability is the probability using all the data (before, during and after). If you consider, for instance, Hamilton's model of GDP growth, the smoothed probability of recession would be the best to compare with NBER definitions, since the NBER decides when recessions begin and end several quarters later and thus use future data as well.
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Fri Jan 27, 2017 11:32 am
by jack
Dear Tom,
Is it posssible to test the statistical significance of the second regime When comparing the regime-switching
GARCH model with the single-regime GARCH model? In the Gray's paper it has been said that The quasi- LRT can no longer be assumed to be distributed as a chi-squared but in this paper
http://onlinelibrary.wiley.com/doi/10.1 ... 3/abstract it has been said that "it is common practice to approximate the critical values of these conventional LR tests by the quantiles of the chi-squared distribution with degrees of freedom equal to the difference in the number of parameters between the two-regimes (alternative) and the single-regime specification (null hypothesis)".
Is it possible finally to use LRT to test the number of Markov regimes?
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Fri Jan 27, 2017 11:58 am
by TomDoan
Sometimes "common practice" is not technically correct and this is one of those cases. I assume the idea is that if the restricted model is overwhelmingly rejected vs the MS model, then the fact that the LRT isn't really chi-squared asymptotically isn't all that important. This
thread is about a calculation of a conservative bound on the LRT in situations like this, but one thing to note is that the MS-GARCH model doesn't compute the actual log likelihood of the model, but only an approximation. I don't know if it's clear whether the approximation understates or overstates the true LL of the model.
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Fri Jan 27, 2017 3:13 pm
by jack
Dear Tom,
I estimated a model using Gray's code. Here is the results. Is there enough evidence about the existence of second regime?
I don't know why P(1,2) is such low. What does is mean here? Especially, why is A12 greater than minus one? Does it has show that something is wrong with the model?
Linear Regression - Estimation by Least Squares
With Heteroscedasticity-Consistent (Eicker-White) Standard Errors
Dependent Variable DRATE
Daily(5) Data From 2003:01:06 To 2012:12:06
Usable Observations 2589
Degrees of Freedom 2587
Centered R^2 0.2162382
R-Bar^2 0.2159353
Uncentered R^2 0.2162382
Mean of Dependent Variable -0.000019215
Std Error of Dependent Variable 0.710001062
Standard Error of Estimate 0.628687695
Sum of Squared Residuals 1022.5071405
Log Likelihood -2471.0231
Durbin-Watson Statistic 2.3494
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. Constant 0.000001372 0.012350981 1.11101e-004 0.99991135
2. DRATE{1} -0.465022692 0.029848275 -15.57955 0.00000000
MAXIMIZE - Estimation by BFGS
Convergence in 14 Iterations. Final criterion was 0.0000048 <= 0.0000100
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1233.4961
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 0.034373643 0.016306202 2.10801 0.03503009
2. A02 -0.018158900 0.005627435 -3.22685 0.00125160
3. A11 -0.987049117 0.024645457 -40.04994 0.00000000
4. A12 -1.036718008 0.031279355 -33.14384 0.00000000
5. B01 0.676242638 0.013864548 48.77495 0.00000000
6. B02 0.178090890 0.005701714 31.23462 0.00000000
7. P(1,1) 0.964435993 0.006934697 139.07400 0.00000000
8. P(1,2) 0.038301809 0.005753795 6.65679 0.00000000
Lag Corr Partial LB Q Q Signif
1 0.089 0.089 20.64769 0.0000
2 0.309 0.303 268.42934 0.0000
3 0.122 0.084 307.28896 0.0000
4 0.101 -0.003 333.89765 0.0000
5 0.082 0.018 351.45483 0.0000
6 0.031 -0.013 354.02735 0.0000
7 0.044 0.006 359.06825 0.0000
8 0.022 0.006 360.29757 0.0000
9 0.055 0.041 368.24714 0.0000
10 0.052 0.040 375.21940 0.0000
11 0.068 0.039 387.30424 0.0000
12 0.089 0.056 408.03453 0.0000
13 0.072 0.028 421.61656 0.0000
14 0.111 0.057 453.70138 0.0000
15 0.091 0.043 475.14533 0.0000
GARCH Model - Estimation by BFGS
Convergence in 31 Iterations. Final criterion was 0.0000059 <= 0.0000100
Dependent Variable DRATE
Daily(5) Data From 2003:01:06 To 2012:12:06
Usable Observations 2589
Log Likelihood -1640.8258
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. Constant -0.002580050 0.004870402 -0.52974 0.59629165
2. DRATE{1} -0.486710196 0.017265759 -28.18933 0.00000000
3. C 0.001934000 0.000469922 4.11558 0.00003862
4. A 0.318002213 0.026901340 11.82105 0.00000000
5. B 0.744130400 0.017127159 43.44739 0.00000000
Lag Corr Partial LB Q Q Signif
1 -0.031 -0.031 2.552248 0.1101
2 0.070 0.069 15.294223 0.0005
3 -0.028 -0.024 17.282169 0.0006
4 -0.015 -0.021 17.855229 0.0013
5 -0.039 -0.037 21.893056 0.0005
6 -0.043 -0.043 26.625084 0.0002
7 -0.036 -0.035 30.074676 0.0001
8 -0.038 -0.037 33.871933 0.0000
9 -0.032 -0.034 36.612003 0.0000
10 -0.001 -0.003 36.617247 0.0001
11 -0.022 -0.025 37.857947 0.0001
12 -0.011 -0.021 38.194854 0.0001
13 -0.012 -0.017 38.548140 0.0002
14 -0.029 -0.037 40.769661 0.0002
15 0.002 -0.006 40.779242 0.0003
MAXIMIZE - Estimation by BFGS
Convergence in 9 Iterations. Final criterion was 0.0000091 <= 0.0000100
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1054.8672
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 0.013619894 0.013106682 1.03916 0.29873196
2. A02 -0.014933917 0.004393704 -3.39894 0.00067649
3. A11 -0.935668475 0.028987754 -32.27806 0.00000000
4. A12 -1.064079366 0.034639104 -30.71902 0.00000000
5. B01 0.067855137 0.006098469 11.12659 0.00000000
6. B11 0.136280582 0.028697956 4.74879 0.00000205
7. B21 0.807379310 0.029557752 27.31532 0.00000000
8. B02 0.003801359 0.000683465 5.56189 0.00000003
9. B12 0.310732981 0.049463576 6.28206 0.00000000
10. B22 0.292483566 0.028278038 10.34313 0.00000000
MAXIMIZE - Estimation by BFGS
Convergence in 21 Iterations. Final criterion was 0.0000094 <= 0.0000100
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1050.5437
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 0.010285521 0.012745732 0.80698 0.41967938
2. A02 -0.015746220 0.004411478 -3.56937 0.00035783
3. A11 -0.934642290 0.030346397 -30.79912 0.00000000
4. A12 -1.085577499 0.037463795 -28.97671 0.00000000
5. B01 0.050692332 0.009910202 5.11517 0.00000031
6. B11 0.157356240 0.031981527 4.92022 0.00000086
7. B21 0.802614140 0.049317631 16.27439 0.00000000
8. B02 0.003374801 0.001166368 2.89343 0.00381063
9. B12 0.229441167 0.070668669 3.24672 0.00116744
10. B22 0.246944292 0.038749720 6.37280 0.00000000
11. P(1,1) 0.960576407 0.013708449 70.07185 0.00000000
12. P(1,2) 0.075710440 0.020554312 3.68343 0.00023011
MAXIMIZE - Estimation by BFGS
NO CONVERGENCE IN 12 ITERATIONS
LAST CRITERION WAS 0.0000000
SUBITERATIONS LIMIT EXCEEDED.
ESTIMATION POSSIBLY HAS STALLED OR MACHINE ROUNDOFF IS MAKING FURTHER PROGRESS DIFFICULT
TRY HIGHER SUBITERATIONS LIMIT, TIGHTER CVCRIT, DIFFERENT SETTING FOR EXACTLINE OR ALPHA ON NLPAR
RESTARTING ESTIMATION FROM LAST ESTIMATES OR DIFFERENT INITIAL GUESSES MIGHT ALSO WORK
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1018.0690
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 -0.013393998 0.000380707 -35.18194 0.00000000
2. A02 0.045332574 0.002076028 21.83620 0.00000000
3. A11 -1.097700039 0.005548809 -197.82625 0.00000000
4. A12 -0.303118795 0.027167144 -11.15755 0.00000000
5. B01 -0.001011178 0.000002767 -365.49626 0.00000000
6. B11 0.059900700 0.000807929 74.14101 0.00000000
7. B21 0.609069171 0.000384612 1583.59479 0.00000000
8. B02 0.019938741 0.000145776 136.77666 0.00000000
9. B12 0.045280994 0.000174983 258.77336 0.00000000
10. B22 1.870801841 0.029521412 63.37101 0.00000000
11. P(1,1) 0.820696725 0.000355251 2310.18726 0.00000000
12. P(1,2) 0.723588475 0.006872191 105.29226 0.00000000
And here is ex ante and smoothed probabilities:
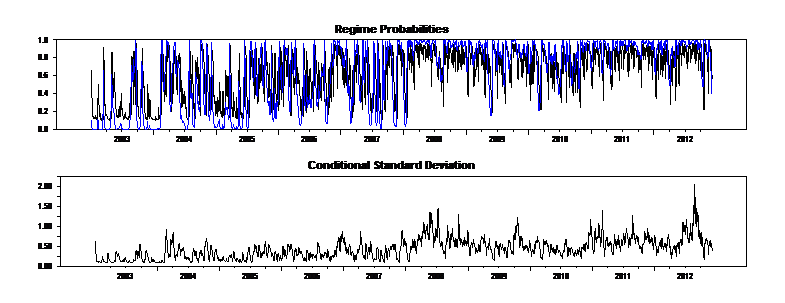
- figure 5.png (28.08 KiB) Viewed 47835 times
Here is the code:
Code: Select all
All of this was out of Gray's paper, "Modeling the conditional
* distribution of interest rates as a regime-switching process", J. of
* Financial Economics 42, 1996, pp 27-62.
*
* Revision Schedule:
* 01/2005 Written by Tom Doan, Estima
* 09/2005 Comments added. Changed to use new %MSSMOOTH procedure
*
OPEN DATA data.xlsx
CALENDAR(D) 2003:1:2
all 2012:12:06
DATA(FORMAT=XLSX,ORG=COLUMNS) 2003:01:02 2012:12:06 rupee rate
set rate = rate*100.0
diff rate / drate
spgraph(vfields=2,window="Figure 3")
graph(header="One Month T-Bill Rates")
# rate
graph(header="One Month T-Bill Yields")
# drate
spgraph(done)
*
* This makes extensive use of the Markov switching functions and
* procedures from MSSetup.src
*
@MSSetup(states=2)
*
* The P and Q values in Gray's notation are handled in MSSetup as an M-1
* x M matrix (called P here), with P(i,j) giving the probabilities of
* moving from state j to state i. The Mth row is implicit, as it's just
* the 1-sum of rest of the column.
*
*******************************************************************************
*
* Table 1 information
*
stats drate
cmom(corr,print)
# drate rate{1}
*******************************************************************************
*
* Table 2 estimates
*
* Single regime is linear regression
*
linreg(robust) drate
# constant drate{1}
*
* We're going to use these later for initial conditions
*
compute olsvar =%seesq
compute olsbeta=%beta
*
* Constant variance regime switching model
* This uses Gray's notation for all the variables other than "P"
*
nonlin a01 a02 a11 a12 b01 b02 p
*
* Initial guess values for MS models are always a bit tricky because the
* model isn't globally identified. This is starting with OLS results for
* state 1 and 0 mean coefficients for state 2.
*
compute a01=olsbeta(1),a11=olsbeta(2),b01=sqrt(olsvar)
compute a02=a12=0.0,b02=b01
*
* The p matrix is initialized to make both states fairly persistent.
* (The 2,2 transition is 1-.1=.9).
*
compute p=||.8,.1||
*
* SimpleRegimeF returns the 2-vector of densities in the two regimes. It
* is specific to the data series used (dependent variable <<drate>>) and
* the precise parameterization, and so would need to be altered slightly
* for a different application. Note that this needs to return the actual
* density, not its log.
*
function SimpleRegimeF t
type vector SimpleRegimeF
type integer t
*
compute SimpleRegimeF=||%density((drate(t)-a01-a11*rate(t-1))/b01)/b01,$
%density((drate(t)-a02-a12*rate(t-1))/b02)/b02||
end
*
* This is the standard log likelihood FRML for a Markov switching model.
*
frml logl = f=SimpleRegimeF(t),fpt=%MSProb(t,f),log(fpt)
@MSFilterInit
maximize(start=(pstar=%MSInit()),method=bfgs,iters=100,pmethod=simplex,piters=5) logl 2 2012:12:06
*
* It's not clear what residuals are used for the diagonostics for the
* regime switching model. The standardized residuals weighted by the ex
* ante probabilities of the two states seem to give LB's which are
* fairly close to those in the paper.
*
set ustd = %dot(pt_t1,||(drate-a01-a11*drate{1})/b01,(drate-a02-a12*drate{1})/b02||)
graph
# ustd
set usqr = ustd^2
@regcorrs(report,number=15) usqr
*
* Compute the smoothed probabilities and the ex ante probabilities
*
@MSSmoothed %regstart() %regend() psmooth
set exante %regstart() %regend() = pt_t1(t)(1)
set smooth %regstart() %regend() = psmooth(t)(1)
*
* And the conditional standard deviation
*
set condstddev = sqrt(exante*b01^2+(1-exante)*b02^2)
*
spgraph(vfields=2,window="Figure 4")
graph(max=1.0,header="Regime Probabilities") 2
# exante
# smooth
graph(header="Conditional Standard Deviation")
# condstddev
spgraph(done)
*******************************************************************************
*
* Table 3 estimates
*
* Single regime GARCH model
*
garch(p=1,q=1,reg,resids=u,hseries=h) / drate
# constant drate{1}
compute onestate=%beta
*
set usqr = u^2/h
@regcorrs(number=15,report) usqr
*
* Regime-switching GARCH
*
nonlin a01 a02 a11 a12 b01 b11 b21 b02 b12 b22 p
compute a01=%beta(1),a11=%beta(2),b01=olsvar,b11=0.0,b21=0.0
compute a02=%beta(1),a12=%beta(2),b02=%beta(3),b12=%beta(4),b22=%beta(5)
compute p=||.95,.05||
*
set uu = olsvar
set h = olsvar
*
* RegimeGARCHF returns the 2 vector of densities in the two regimes.
* Again, many lines in this are specific to the problem at hand.
*
function RegimeGARCHF t
type vector RegimeGARCHF
type integer t
local real hh1 hh2 mu1 mu2 mu
*
* Compute state dependent variances
*
compute hh1=b01+b11*uu(t-1)+b21*h(t-1)
compute hh2=b02+b12*uu(t-1)+b22*h(t-1)
*
* Compute state dependent means
*
compute mu1=a01+a11*rate(t-1)
compute mu2=a02+a12*rate(t-1)
*
* Compute the return vector (densities in the two states)
*
compute RegimeGARCHF=||%density((drate(t)-mu1)/sqrt(hh1))/sqrt(hh1),$
%density((drate(t)-mu2)/sqrt(hh2))/sqrt(hh2)||
*
* Compute the values of uu (squared residual) and h (variance) to be
* used for the period following.
*
compute mu=mu1*pstar(1)+mu2*pstar(2)
compute uu(t)=(drate(t)-mu)^2
compute h(t)=pstar(1)*(mu1^2+hh1)+pstar(2)*(mu2^2+hh2)-mu^2
end
*
frml logl = f=RegimeGARCHF(t),fpt=%MSProb(t,f),log(fpt)
*
* This combination is able to locate Gray's results - the first MAXIMIZE
* works with the "p" matrix fixed at a fairly high level of persistence,
* and tries to get estimates which separate the two states. The second
* then adds the p matrix to the parmset.
*
nonlin a01 a02 a11 a12 b01 b11 b21 b02 b12 b22
maximize(start=(pstar=%MSInit()),method=bfgs,iters=100,pmethod=simplex,piters=50) logl 2 2012:12:06
nonlin a01 a02 a11 a12 b01 b11 b21 b02 b12 b22 p
maximize(start=(pstar=%MSInit()),method=bfgs,iters=100) logl 2 2012:12:06
*
* Compute the smoothed probabilities and the ex ante probabilities
*
@MSSmoothed %regstart() %regend() psmooth
set exante %regstart() %regend() = pt_t1(t)(1)
set smooth %regstart() %regend() = psmooth(t)(1)
*
* And the conditional standard deviation
*
set condstddev = sqrt(h)
*
spgraph(vfields=2,window="Figure 5")
graph(max=1.0,header="Regime Probabilities") 2
# exante
# smooth
graph(header="Conditional Standard Deviation")
# condstddev
spgraph(done)
*
*
* However, this set of initial guess values (which are actually the
* result of a typo in trying to reproduce the article's numbers) find a
* local max with quite a bit higher likelihood, and dramatically
* different behavior. How one might find this systematically is unclear.
*
compute a01=.1407,a02=-.0011,a11=-.0141,a12=.0006,b01=.0004,b11=.4609,b21=.1977,b02=.0099,b12=.1655,b22=.2685,p=||.9739,1-.9896||
maximize(start=(pstar=%MSInit()),method=bfgs,iters=100,pmethod=simplex,piters=50) logl 2 2012:12:06
*******************************************************************************
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Fri Jan 27, 2017 6:36 pm
by TomDoan
You realize the Gray was analyzing US interest rates and his model was chosen for that. I have no idea what your series is, but it has very different dynamics than Gray's. Your results suggest that your mean model is wrong---you're showing signs of overdifferencing.
There's absolutely nothing wrong with a small P(1,2), that means P(2,2) is fairly large, so both regimes are persistent, which isn't that unusual. However, it looks like a MS model is overkill. There appears to be a structural break about at the midpoint of your sample, and the MS is simply picking that up.
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Sat Jan 28, 2017 2:33 pm
by jack
Dear Tom,
I adjusted the model and here is the result. My data is exchange rate return. In the first regime, there is negative first order correlation (A11) but it is positive in the second regime (A12). And in the simple model here isn't any correlation. Isn't it strange?
Statistics on Series RATE
Daily(5) Data From 2003:01:02 To 2012:12:06
Observations 2591
Sample Mean 0.009871 Variance 0.254899
Standard Error 0.504875 SE of Sample Mean 0.009919
t-Statistic (Mean=0) 0.995250 Signif Level (Mean=0) 0.319708
Skewness 0.204085 Signif Level (Sk=0) 0.000022
Kurtosis (excess) 5.843007 Signif Level (Ku=0) 0.000000
Jarque-Bera 3703.762694 Signif Level (JB=0) 0.000000
Correlation Matrix
RATE RATE{1}
RATE 1.0000000000 0.0119264167
RATE{1} 0.0119264167 1.0000000000
Linear Regression - Estimation by Least Squares
With Heteroscedasticity-Consistent (Eicker-White) Standard Errors
Dependent Variable RATE
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Degrees of Freedom 2588
Centered R^2 0.0001422
R-Bar^2 -0.0002441
Uncentered R^2 0.0005240
Mean of Dependent Variable 0.0098672569
Std Error of Dependent Variable 0.5049725654
Standard Error of Estimate 0.5050341946
Sum of Squared Residuals 660.09408372
Log Likelihood -1904.7459
Durbin-Watson Statistic 1.9986
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. Constant 0.0097490582 0.0098791820 0.98683 0.32372673
2. RATE{1} 0.0119265083 0.0328551991 0.36300 0.71660327
MAXIMIZE - Estimation by BFGS
Convergence in 9 Iterations. Final criterion was 0.0000046 <= 0.0000100
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1233.4961
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 0.034375380 0.018717432 1.83654 0.06627729
2. A02 -0.018159015 0.005528836 -3.28442 0.00102193
3. A11 0.012948320 0.025544213 0.50690 0.61222612
4. A12 -0.036714468 0.030673547 -1.19694 0.23132901
5. B01 0.676243274 0.014175432 47.70530 0.00000000
6. B02 0.178091226 0.005170468 34.44393 0.00000000
7. P(1,1) 0.964435901 0.006035214 159.80145 0.00000000
8. P(1,2) 0.038300888 0.005961810 6.42437 0.00000000
Lag Corr Partial LB Q Q Signif
1 0.0339 0.0339 2.988551 0.0839
2 0.0330 0.0319 5.815595 0.0546
3 0.0209 0.0188 6.950812 0.0735
4 0.0580 0.0558 15.691318 0.0035
5 0.0679 0.0634 27.684503 0.0000
6 0.0430 0.0356 32.499693 0.0000
7 0.0521 0.0445 39.564417 0.0000
8 0.0292 0.0194 41.786765 0.0000
9 0.0177 0.0056 42.605573 0.0000
10 0.0320 0.0206 45.269952 0.0000
11 0.0659 0.0541 56.593080 0.0000
12 0.0233 0.0090 58.003813 0.0000
13 0.0301 0.0184 60.358844 0.0000
14 0.0519 0.0414 67.379388 0.0000
15 0.0336 0.0184 70.331039 0.0000
GARCH Model - Estimation by BFGS
Convergence in 23 Iterations. Final criterion was 0.0000041 <= 0.0000100
Dependent Variable RATE
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Log Likelihood -1106.0489
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. Constant -0.009116152 0.004583112 -1.98907 0.04669295
2. RATE{1} 0.035172878 0.022646726 1.55311 0.12039663
3. C 0.001088115 0.000282215 3.85562 0.00011543
4. A 0.246598747 0.026254036 9.39279 0.00000000
5. B 0.791129966 0.018299852 43.23150 0.00000000
Lag Corr Partial LB Q Q Signif
1 0.053 0.053 7.155283 0.0075
2 -0.008 -0.011 7.314639 0.0258
3 -0.024 -0.023 8.800338 0.0321
4 0.032 0.035 11.463173 0.0218
5 -0.005 -0.009 11.533096 0.0418
6 -0.030 -0.030 13.918315 0.0306
7 -0.030 -0.025 16.257684 0.0229
8 -0.024 -0.023 17.751739 0.0232
9 -0.031 -0.030 20.225390 0.0166
10 -0.016 -0.012 20.850930 0.0222
11 -0.026 -0.025 22.658262 0.0197
12 -0.019 -0.018 23.600898 0.0230
13 -0.027 -0.026 25.444931 0.0202
14 -0.039 -0.040 29.388071 0.0093
15 -0.037 -0.036 32.917932 0.0048
MAXIMIZE - Estimation by BFGS
Convergence in 2 Iterations. Final criterion was 0.0000050 <= 0.0000100
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1054.0329
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 0.013549085 0.012540572 1.08042 0.27995519
2. A02 -0.014930348 0.004370346 -3.41629 0.00063482
3. A11 0.064567104 0.029604611 2.18098 0.02918480
4. A12 -0.064066500 0.034049382 -1.88158 0.05989361
5. B01 0.067479479 0.005412803 12.46664 0.00000000
6. B11 0.135819468 0.013344841 10.17768 0.00000000
7. B21 0.808728790 0.017795344 45.44609 0.00000000
8. B02 0.003753066 0.000429312 8.74204 0.00000000
9. B12 0.312228200 0.047843182 6.52608 0.00000000
10. B22 0.294668993 0.019177199 15.36559 0.00000000
MAXIMIZE - Estimation by BFGS
Convergence in 22 Iterations. Final criterion was 0.0000006 <= 0.0000100
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1049.7041
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 0.010332656 0.012722085 0.81218 0.41668686
2. A02 -0.015752333 0.004410645 -3.57144 0.00035503
3. A11 0.066010875 0.030439228 2.16861 0.03011215
4. A12 -0.086271210 0.037563514 -2.29668 0.02163728
5. B01 0.050481058 0.009854571 5.12260 0.00000030
6. B11 0.156253488 0.032079328 4.87085 0.00000111
7. B21 0.805724006 0.051333920 15.69574 0.00000000
8. B02 0.003278824 0.001207730 2.71487 0.00663027
9. B12 0.229633335 0.069779573 3.29084 0.00099889
10. B22 0.249913547 0.039345596 6.35175 0.00000000
11. P(1,1) 0.959801475 0.014292487 67.15427 0.00000000
12. P(1,2) 0.076891035 0.021664827 3.54912 0.00038652
MAXIMIZE - Estimation by BFGS
NO CONVERGENCE IN 24 ITERATIONS
LAST CRITERION WAS 0.0000000
SUBITERATIONS LIMIT EXCEEDED.
ESTIMATION POSSIBLY HAS STALLED OR MACHINE ROUNDOFF IS MAKING FURTHER PROGRESS DIFFICULT
TRY HIGHER SUBITERATIONS LIMIT, TIGHTER CVCRIT, DIFFERENT SETTING FOR EXACTLINE OR ALPHA ON NLPAR
RESTARTING ESTIMATION FROM LAST ESTIMATES OR DIFFERENT INITIAL GUESSES MIGHT ALSO WORK
Daily(5) Data From 2003:01:03 To 2012:12:06
Usable Observations 2590
Function Value -1009.2015
Variable Coeff Std Error T-Stat Signif
************************************************************************************
1. A01 -0.019277002 0.000748007 -25.77117 0.00000000
2. A02 0.029994572 0.000048554 617.75949 0.00000000
3. A11 -0.134259201 0.001260581 -106.50579 0.00000000
4. A12 0.526709694 0.050463318 10.43748 0.00000000
5. B01 -0.001186886 0.000009806 -121.03180 0.00000000
6. B11 0.081255446 0.002636271 30.82211 0.00000000
7. B21 0.523741479 0.003905943 134.08835 0.00000000
8. B02 0.016741849 0.000448428 37.33451 0.00000000
9. B12 0.070595091 0.019397509 3.63939 0.00027329
10. B22 1.679419320 0.037539345 44.73758 0.00000000
11. P(1,1) 0.746300187 0.000065127 11459.07867 0.00000000
12. P(1,2) 0.611475906 0.015966929 38.29640 0.00000000
Following figure shows ex ante and smoothed probabilities. Introduction of exchange rate futures took place on April 23, 1990 . Can one say that this event has increased the volatility of market? Or it has had a destabilizing effect on the market?
Can I have this figure to be shaded after this time? How can I have LB statistic for squared residuals of Regime-switching GARCH?
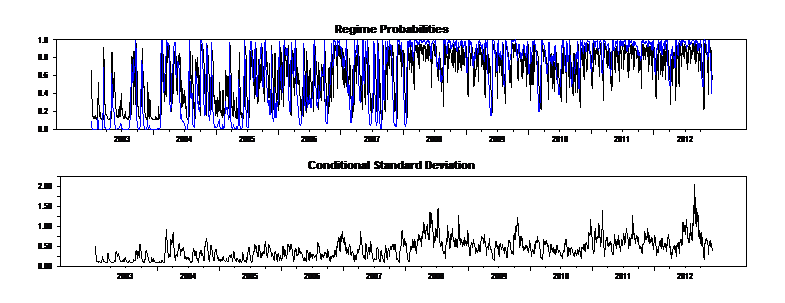
- figure 5.png (27.54 KiB) Viewed 47825 times
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Sat Jan 28, 2017 8:53 pm
by TomDoan
If something happened in April 1990 and your data set starts in 2003, how do you think that your results will show anything?
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Sun Jan 29, 2017 12:28 am
by Catife
Dear Tom,
I have some questions about the part of time-varying transition probabilities (TVTP) in the sample codes.
The first question is about the calculations of pt_t, pt_t1, and smoothed probabilities after estimating the TVTP model of Gray (1996). Based on my understanding, hamilton filter still works in this case since Gray (1996)'s TVTP setup is still based on lagged information. However, when I estimate the TVTP part, I find the calculated pt_t, pt-t1, and smoothed probabilities are not informative in terms of that they fluctuate around 0.3-0.4 for one regime over time. Are these proper outcomes or the hamilton filter should be changed accordingly in this case?
The second question is the difference between Filardo (1994) and Gray (1996) regarding the TVTP parts of them. In the sample codes of Filardo (1994) you provided, there is a formal function (%msvarpmat) which is re-defined to accommodate TVTP in the codes. On the other hand, the sample codes of Gary (1996) only override the transition matrix when we formulate the likelihood function. Is there a reason to set up TVTP differently, given the TVTP are defined similarly in these two papers from my view?
I will appreciate your replies and comments. Thank you very much.
Best Regards
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Sun Jan 29, 2017 3:32 am
by jack
I'm really sorry. The event took place in April, 2008.
Re: Gray JFE 1996 Markov Switching GARCH model
Posted: Mon Jan 30, 2017 11:20 am
by TomDoan
If you have a particular date of interest, why are you doing a MS model? That's completely wrong for that. Just concentrate on the differences in the model before and after the policy change.