Page 1 of 2
Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Fri Jun 15, 2018 9:58 am
by swnzh86
Dear all,
I would like to use the code of Diebold Rudebusch Aruoba (2006) (yield-macro dynamic term structure model) to examine the effects of unconventional monetary policy in the euro area.
As the first step, I try to replicate of the results of the reference paper to test the correctness of the RATS-code drajoe2006.
However, everything is fine until I try to replicate the impulse response functions using the command
@dlmirf(a=a,f=sw,steps=30,variables=||"L Response","S Response","C Response","CU Response","FFR Response","INFL Response"||,shocks=||"Shock to L","Shock to S","Shock to C","Shock to CU","Shock to FFR","Shock to INFL"||,results=IRFGRAPH)
In the attachment there are the estimated IRF and the IRF from the paper.... Why is my result different from that of the paper?
Thanks
P.S How can be the error bands constructed?
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Fri Jun 15, 2018 12:21 pm
by TomDoan
F=SW in the RATS code is definitely not right---SW is the covariance matrix and so has shocks squared (in effect). I'm not 100% sure what their IRF's show. Offhand, it looks like they're doing a Cholesky factor normalized so unit diagonals, though the 5,6 graph doesn't fit that. If that's simply an error, computing
compute fsw=%decomp(sw)
compute fsw=%ddivide(fsw,%diag(fsw))
and then doing the @DLMIRF with F=FSW (and everything else the same) should come pretty close.
It looks like they do "analytical" error bands, which is a very complicated calculation.
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Mon Jun 18, 2018 5:43 am
by swnzh86
Dear Tom,
Thanks for the reply! Now the impulse responses are in line with these in the reference paper.
Do you have any ideas how the error bands could be constructed, or is there any literature on that?
Thanks
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Mon Jun 18, 2018 7:50 am
by TomDoan
That's in a technical appendix of the working paper. Isn't it in the published paper as well?
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Mon Jun 18, 2018 10:11 am
by swnzh86
Oh yes, you're right. I will try to implement the error bands in RATS. Thanks Tom!
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Tue Nov 06, 2018 10:29 am
by swnzh86
Hi Tom,
After some attempts, the Delta method described in the Diebold, Rudebusch and Aruoba (2006) paper for constructing error bands of state space IRFs seems to be very difficult to implement.....
Is their a way to implement
1. Monte-Carlo or Bootstrapping methods for DLMIRF by using/modifying "bootvar" and "mcgraphirf" procedures?
2. the Delta method by modifying "VARIRFDelta" procedure?
Thanks!
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Tue Nov 06, 2018 1:32 pm
by TomDoan
No. This is a state-space model, not a VAR. Gibbs sampling for state-space models (which is what you would need to use) is covered in detail in the 2nd edition of the
State-Space/DSGE e-course.
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Tue Nov 06, 2018 2:06 pm
by swnzh86
Dear Tom,
Thanks for the reply.
Since the transition equation is basically a VAR(1) model, the formula of the IRF function "DLMIRF" is the same as in DRA(2006) which is a normal IRF (See Appendix A.1.2).
A.1.2 also provides the Delta method for estimating the asymptotic standard errors of IRF....
Is it really not possible to modify the code of "VARIRFDelta"?
I have written a modified Version of VARIRFDelta. I would be grateful if you can take a look.
Thanks!
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Tue Nov 06, 2018 3:35 pm
by TomDoan
No. While the transition matrix may be in the form of a VAR, it's a VAR in unobservable variables, with the mapping from unobservables to observables depending upon a small number of parameters. The various VAR-specific procedures are for VAR's strictly on observables with no restrictions.
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Wed Nov 07, 2018 7:50 am
by swnzh86
Dear Tom,
I used my modified VARIRFDelta and got the same confidence bands for every impulse response as in DRA2006....
The problem now is when the impulse responses should be plotted altogether, the loop below only estimates the last confidence band of the last impulse response (see attachment, right corner).
Here is my code:
declare rect[series] upper_matrix(6,6)
do i=1,6
do j=1,6
set upper_matrix(i,j) 1 31 = 0.0
end do j
end do i
declare rect[series] lower_matrix(6,6)
do i=1,6
do j=1,6
set lower_matrix(i,j) 1 31 = 0.0
end do j
end do i
do i = 1,6
do j = 1,6
do h = 1,31
@VARIRFDelta(a=a,h=h,shock=||1.0,1.0,1.0,1.0,1.0,1.0||,nvar=6,nreg=6) covxx
set upper_matrix(i,j) h h = IRFGRAPH(i,j)(h)+sqrt(covxx(i,i))*1.96
set lower_matrix(i,j) h h = IRFGRAPH(i,j)(h)-sqrt(covxx(i,i))*1.96
end do h
end do j
end do i
I don't see any index problem in my loop....
Sorry for keeping asking questions, but it would be really nice if you can point out any problems in the Code.
Thanks
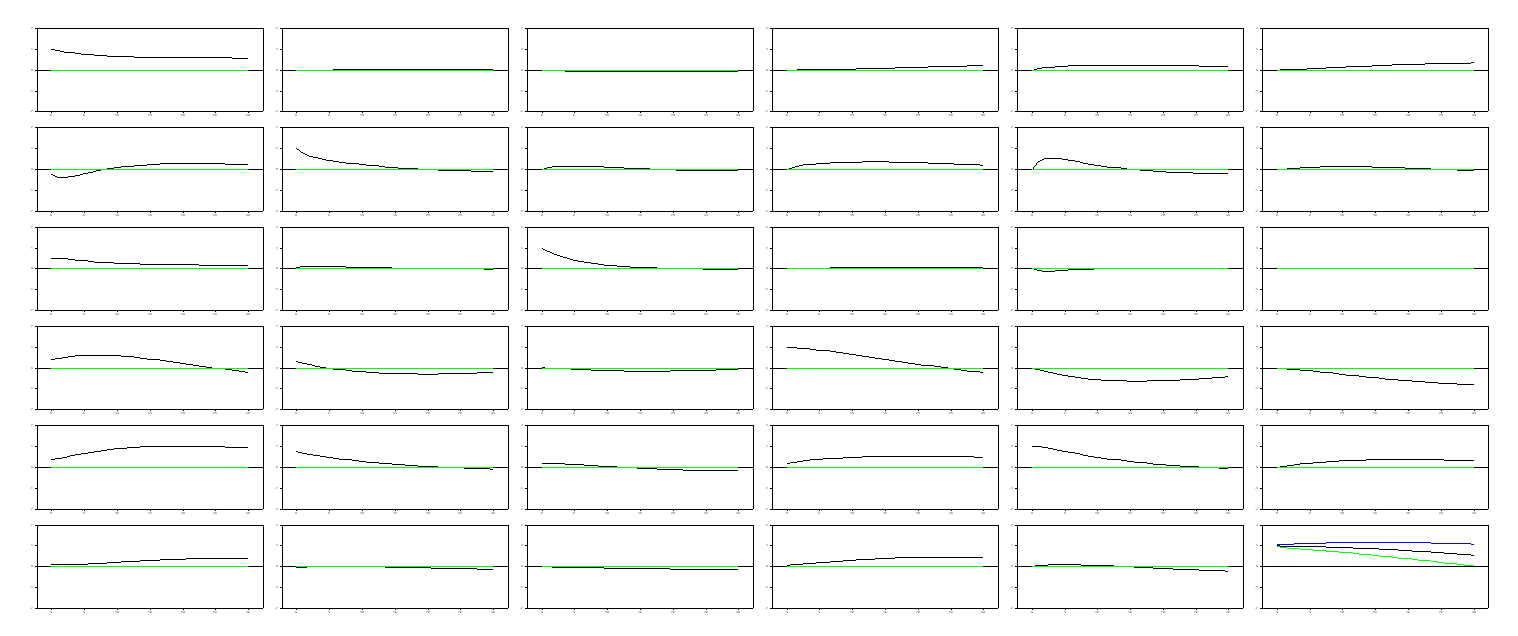
- irf.PNG (18.88 KiB) Viewed 23865 times
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Wed Nov 07, 2018 9:10 am
by TomDoan
What is this supposed to mean? Shouldn't the shock be to element j?
shock=||1.0,1.0,1.0,1.0,1.0,1.0||
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Wed Nov 07, 2018 9:44 am
by swnzh86
Changing to the correct shock %unitv(nvar,j) doesn't help..... Still the only the error bands of the last IRF is estimated.
I think the problem lies in the loop structure....
For the modified VARIRFDelta.... Essentially I changed the %sigma in the code to the sw which is the covariance matrix of the transition shock and %xx to inv(tr(X)*X) which is related to the extracted factors from the states (see
https://estima.com/forum/viewtopic.php?f=8&t=1028 for pulling out the factors)
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Wed Nov 07, 2018 10:06 am
by TomDoan
I'm not even sure what you're saying. From what I can see, you are getting no confidence bands at all---it looks like the response and a series (probably two series) of zeros.
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Wed Nov 07, 2018 11:17 am
by swnzh86
Sorry I didn't make the problem clear.
I can estimate the confidence bands using the modified VARIRFDelta.
As an example, here is a replication of an IRF of DRA(2006) in Figure 5 (Shock from Federal Funds Rate to Inflation, paper in attachment):
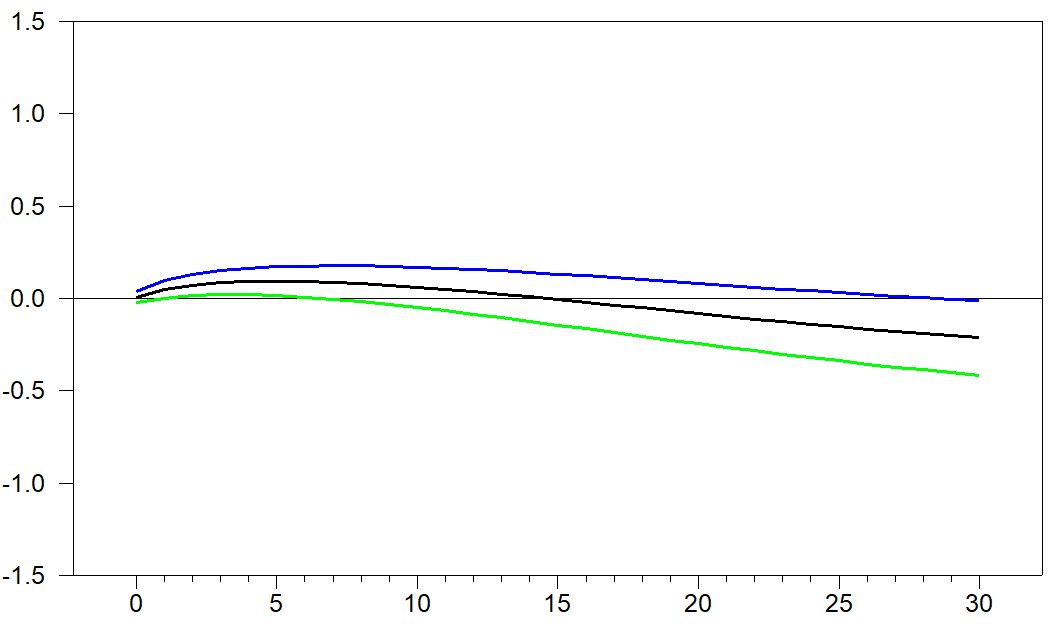
- irf.PNG (10.69 KiB) Viewed 23857 times
However, my problem is, if I try to plot all the impulse responses + error bands at the same time by using the following loop:
do i = 1,6
do j = 1,6
do h = 1,31
@VARIRFDelta(a=a,h=h,shock=||1.0,1.0,1.0,1.0,1.0,1.0||,nvar=6,nreg=6) covxx
set upper_matrix(i,j) h h = IRFGRAPH(i,j)(h)+sqrt(covxx(i,i))*1.96
set lower_matrix(i,j) h h = IRFGRAPH(i,j)(h)-sqrt(covxx(i,i))*1.96
end do h
end do j
end do i
Only the error band of the last response (see the Shock from Inflation to Inflation, the lower right hand corner of the figure from the my second last post) is estimated, and for the rest, yes, no confidence bands.
Re: Replicate IRF in Diebold Rudebusch Aruoba (2006)
Posted: Wed Nov 07, 2018 1:57 pm
by TomDoan
You're not showing the part of the code that does the graphs.