DLMIRFEXAMPLE.RPF

DLMIRFEXAMPLE.RPF demonstrates use of the @DLMIRF procedure for doing impulse responses in a state-space model.

Full Program

*
* Model with linear production and quadratic utility
*
dec real beta f u1 u2
*
* Endogenous series
*
dec series c k
*
frml(identity) f1 = beta*f*(u1-u2*c{-1})-(u1-u2*c)
frml           f2 = (k+c)-f*k{1}
*
* Pegging parameters
*
compute beta   =.99   ;* discount factor
compute f      =1.02
compute u1     =1.0
compute u2     =0.5
*
group bliss f1 f2
dsge(model=bliss,a=adlm,f=fdlm,z=zdlm) c k
@dlmirf(a=adlm,f=fdlm,steps=24,nograph,results=linearf)
*
* Using log rather than quadratic utility, and decreasing returns
* production function.
*
declare series c k y r theta
declare real beta f alpha delta
*
compute beta =.99
compute alpha =.7
compute f     =5.0
compute delta =.15
*
frml(identity) f1 = beta*r{-1}*c/c{-1}-1.0
frml(identity) f2 = r-alpha*f*k{1}^(alpha-1)*theta
frml(identity) f3 = y-f*k{1}^alpha*theta
frml(identity) f4 = k+c-(y+(1-delta)*k{1})
frml           f5 = log(theta)
*
group nonlin f1 f2 f3 f4 f5
dsge(model=nonlin,expand=loglinear,a=adlm,f=fdlm,z=zdlm,steady=ss) c k r y theta
*
@dlmirf(a=adlm,f=fdlm,steps=24,nograph,results=cobbdouglasf)
*
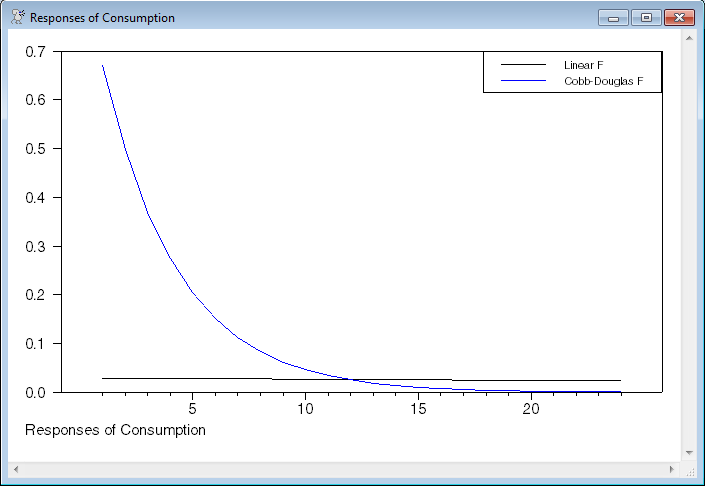
graph(footer="Responses of Consumption",key=upright,klabels=||"Linear F","Cobb-Douglas F"||) 2
# linearf(1,1)
# cobbdouglasf(1,1)
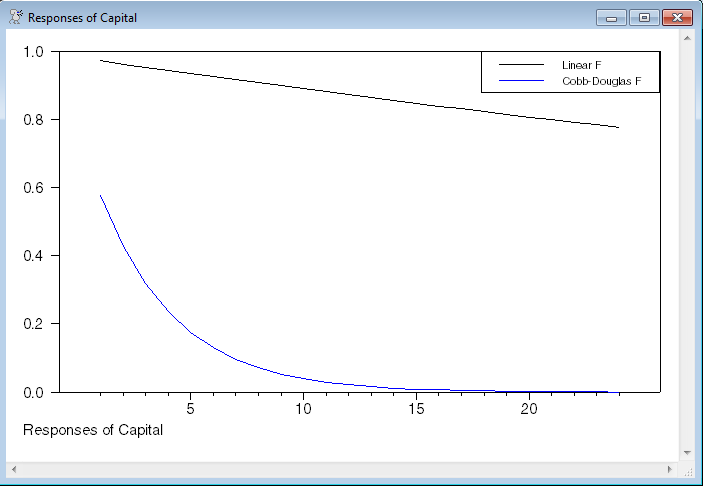
graph(footer="Responses of Capital",key=upright,klabels=||"Linear F","Cobb-Douglas F"||) 2
# linearf(2,1)
# cobbdouglasf(2,1)

Graphs